for Continuous Media Servers

Crowne Plaza Hotel, Seattle, USA

Large scale clustered continuous media (CM) servers deployed in applications like video-on-demand have high availability requirements. In the event of server failure, streams from the failed servers must be reassigned to healthy servers with minimum service disruption. Such servers may also suffer from periods of transient overload resulting from a high degree of customer interactivity. For example, in a video-on-demand system if a large number of users are viewing a favorite game, many of them can simultaneously request a replay of an interesting part of the game. This requires a large number of ``interactive'' channels within a short period of time and can result in a transient server overload. In this paper we propose solutions for graceful recovery from overload scenarios arising out of server failure or customer interactions. Rapid resource reclamation is key to overload tolerance, and our proposed solution is based on rate adaptive stream merging and content insertion techniques. We also utilize conventional time-sharing techniques to handle transient overload. We show that while merging is necessary for achieving overload tolerance, it is not sufficient, and for a complete solution, content insertion is required. Specifically, we consider a general clustered CM server architecture model where multiple servers can fail simultaneously. We develop a model for resource shortfalls that occur as a result of overload on failure. We also describe optimal polynomial time algorithms for recovering resources to the maximum extent possible, by clustering streams in real time.
Overload tolerance, fault tolerance, clustered video servers, interactive video-on-demand, content insertion, rate adaptive stream merging, stream clustering, caching.
In conventional file servers and operating systems, on failure or on overload, clients wait until service is resumed. This is unacceptable for continuous media (CM) applications. In particular, with video it is necessary that content is continuously available to the viewer even on the event of server failure.
Consider the following analogy of a movie theater. In the event of a projector failure, it would be far more desirable to watch a preview of another movie than to stare at a blank screen, especially if the failure persists for a long time. In other words, it may be acceptable under failure conditions to alter the presentation in some reasonable way that does not significantly affect the users. This indicates that the definitions of fault resilience must be rethought for emerging technologies such as digital video broadcasting, that is, the structure of data can be reorganized and altered to meet a desired quality of presentation, measured by the continuity of presentation. Clearly, this assumption must be validated against the application being evaluated. Inserting arbitrary content would be extremely catastrophic for an application such as medical imaging where the correctness of data is more important than the visual experience. However, a majority of home edutainment (education + entertainment) applications can take advantage of content modification techniques and it is these that we consider in this paper.
Video, as a visual medium, is relatively resilient to data corruption due to the high amount of redundancy in visual information. Fault recovery techniques that take advantage of this observation can be classified into two broad categories: (i) Techniques that alter content and (ii) Techniques that drop information. Fundamentally, both techniques achieve fault resilience by reducing the resources required by a video stream (measured by its bandwidth). Content alteration techniques take advantage of the intra-image redundancy whereas frame-dropping techniques take advantage of inter-image redundancy [9,10,12]. An alternate approach is to provide fault resilience by building redundancy into the system as in RAID based servers [2,10,9].
Rate-adaptation and stream manipulation require some content to be dropped [6,12,3]. Furthermore, these schemes tend to be either CPU intensive or require a significant time to achieve the desired reduction in resource utilization. RAID based techniques to handle overload typically involve over-allocation of resources. In large systems, introducing redundancies for correcting errors as well as for fault tolerance is expensive. Furthermore, over-allocation of resources to handle overload is clearly not economical. It is therefore desirable to develop a scheme that makes efficient use of resources yet recovers gracefully under failure with a minimum impact to the user.
In this paper, we introduce content insertion as a means to reclaim resources and recover from overloads arising out of a fault condition. Most of the current work in the field address the overload problem by degrading the quality of service to the user, for example by dropping information content to recover system bandwidth resources. This does not meet the requirements of the media broadcasting industry. Additionally, they do not consider the suitable ``reflex-response'' that is required to ensure continuity of presentation to the user. We perceive that the paradigm of ``sharing'' of resources is better than ``rationing'' of resources. Content insertion is an efficient and practical alternative that provides a mechanism to easily implement sharing of resources. More important, it can be easily adapted to work in conjunction with the other conventional techniques described earlier.
In content insertion, users are presented with an alternative media stream during overload or fault conditions while the fault recovery mechanism is activated. The advantage here is that multiple users can be placed on the same channel thus conserving resources. The new content can contain advertisements or previews and can subsidize customer subscription costs.
We focus on building such a fault recovery scheme in a storage server, but the solutions can be applied easily to other components such as the network. If the network gets congested, users can be temporarily placed on broadcast channels until the congestion subsides. Such a scheme is vastly preferable to a scheme where content is dropped, resulting in a choppy presentation. A user's quality-of-service (QoS) is now measured by how often a user sees an advertisement in the event of failure or overload. A premium user would always have the desired bandwidth by paying more (except of course, in the presence of a catastrophic failure). This strategy is similar to the current CATV/DSS paradigm where users pay extra for subscribing to premium channels for the privilege of viewing programs with few interruptions.
The main focus of this paper is the use of rate adaptive stream merging and content insertion to provide overload tolerance. We design a mechanism that recovers the maximum amount of resources in a given amount of time with minimum impact to the clients and is fair to the clients. The rest of the paper is organized as follows. Section 2 provides the necessary background on resource reclamation techniques for continuous media servers and establishes the basis for our work. In Section 3 we develop a formal model of our system and then analyze recoverability under different overload scenarios. The gains from the proposed mechanism are quantified in Section 4. Section 5 is a discussion of the associated trade-offs. Section 6 summarizes the ideas presented.
In this section, we describe a general architecture for a clustered CM server. We introduce the techniques of batching and clustering using rate adaptive stream merging and content insertion, all of which are related to our proposed scheme for overload recovery.
Consider a general clustered video server architecture as shown in
Figure 1. The system consists of several
servers that disseminate content to clients via a delivery
network. The delivery network consists of many channels that
are accessible to all the clients. This model is typical for most
real world systems.
Large-scale storage servers are built as monolithic units with large
caches, inherent fault tolerance and are designed to meet high
availability requirements. User transactions are handled by a cluster
of front-end I/O processors that can access all the stored content.
This model is typical for most
real world systems.
Large-scale storage servers are built as monolithic units with large
caches, inherent fault tolerance and are designed to meet high
availability requirements. User transactions are handled by a cluster
of front-end I/O processors that can access all the stored content.
Typically, any server can transmit on any channel but no two servers can use a particular channel at the same time and we assume the presence of a mechanism to ensure this mutual exclusion. It is in many ways similar to a CATV architecture but is general enough to accommodate a packet switched network in which channels can be implemented via multicast groups. Any channel in use would carry exactly one program stream. Furthermore, it is straightforward to implement some dedicated channels that continuously transmit advertisements, news clips or other programs of general interest. These channels permit content insertion in real-time and play an important role in the fault recovery scheme described in greater detail in Section 3. We now survey some of the schemes proposed in literature for resource reclamation in continuous media servers and discuss the applicability of these schemes for recovery from overload.
In batching, new playout requests for streams are grouped together at the time of request and channels are allocated to groups of users. With batching clients may have an initial waiting period which can cause them to renege their requests. Clients can be blocked due to all channels being consumed. The impact of channel allocation policies on quality of service in the CATV context is analyzed by Nussbaumer et al. [8]. Batching works well as long as the users do not interact. However, interactions cause users to break away from their groups defeating the initial gains. Such break-aways must be handled by starting a new independent stream for the user requesting interaction by drawing from a pool of contingency channels. A model for optimally allocating channels for batching, on-demand playback and contingency has been developed by Dan et al. [5].
When all contingency channels are consumed, any user interaction will block. This is an event which would occur with a very small but finite probability. This cannot be altogether avoided due to the statistical nature of the allocation policy. Periods of high interactivity can deplete all the free channels available and no more users can be admitted nor user interaction be permitted until some streams exit. This is a serious disadvantage of initial batching. Such situations can also be interpreted as a server overload in the context of this paper.
Rate adaptive stream merging (or adaptive piggy-backing) [6]
is a technique that attempts to merge streams by varying their display rates.
It has been observed that rate changes of 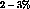 by frame interpolation and
expansion or contraction of the total length of the movie by up to
by frame interpolation and
expansion or contraction of the total length of the movie by up to 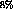 are
acceptable in commercial video playback [6]. Content progression
rates are distinct from the data delivery rate or the frame rate. An
accelerated content progression rate implies that the total duration of the
video will be reduced and any given scene would occur earlier in time.
are
acceptable in commercial video playback [6]. Content progression
rates are distinct from the data delivery rate or the frame rate. An
accelerated content progression rate implies that the total duration of the
video will be reduced and any given scene would occur earlier in time.
Stream merging policies for resource reclamation in a healthy server are considered in [6]. Rate adaptive merging of streams reduces resource requirements both at the server and in the network. Batching can also be used in conjunction with merging for increased gains. We will now illustrate the process of rate adaptive merging with two streams carrying the same program [6].
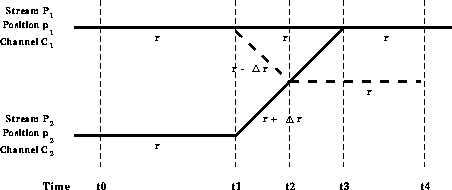
Figure 2: Rate Adaptive Merging of Streams
In Figure 2, at time 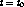 , the streams
, the streams  and
and
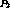 carry the same program at rate r but with a temporal skew. Let
the streams be at positions
carry the same program at rate r but with a temporal skew. Let
the streams be at positions  and
and 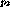 respectively at time
respectively at time  . Let
. Let 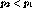 , and the positions are measured in terms of access
units, like video frames for instance. By accelerating the content
progression rate of stream
, and the positions are measured in terms of access
units, like video frames for instance. By accelerating the content
progression rate of stream 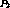 by setting it to
by setting it to 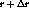 at
time
at
time  , we can make the two streams reach the same point in
the program at time
, we can make the two streams reach the same point in
the program at time 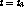 . The catch-up window is determined
by the time interval :
. The catch-up window is determined
by the time interval :
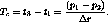
The minimum duration of  is constrained by the maximum change allowed
in the content progression rate. It is possible (see Section
5) to set the content progression rate of
stream
is constrained by the maximum change allowed
in the content progression rate. It is possible (see Section
5) to set the content progression rate of
stream  to
to  at time
at time  and make the streams
reach the same point in the program earlier, at time
and make the streams
reach the same point in the program earlier, at time  and the
merging time interval
and the
merging time interval 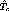 in this case is given by,
in this case is given by,
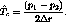
Depending on the rate adaptation policy, the streams reach an identical
state at  or
or  . At this point all clients receiving stream
. At this point all clients receiving stream  can be transferred to stream
can be transferred to stream  and the resources associated with
and the resources associated with  can be released.
can be released.
The size of the catch-up window is severely constrained by the maximum acceleration rate permissible from QoS considerations. If we wish to use merging in order to release channels in the event of failure, no resources are freed during the period of the catch-up window, which can be significantly long. If we wish to merge a failed stream, we allocate additional resources for it until it gets merged. It is likely that extra resources are unavailable in the event of failure and this shortfall can be significant when a large number of failed streams must be recovered. The next section elaborates on how content insertion techniques address this problem.
Content insertion can be viewed as a coarse grained rate adaptation technique. This is the informational view -- the primary content rate is altered by the introduction of secondary content. The secondary content can take the form of other programming. A different and operational view would explain content insertion as a form of intermediate batching. A third view arising from scheduling would explain the same technique as time-sharing. All these different views influence the application of content insertion in our proposed scheme.
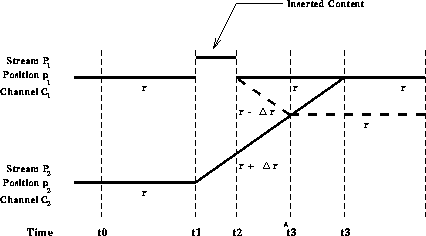
Figure 3: Modifying the Catch-Up Window through Content Insertion
Although television commercials are considered annoying by many, they subsidize the cost of entertainment provided to the consumer. With VOD services, these advertisements can lower per-user costs in an entirely new way by helping to diminish the number of concurrent streams via intermediate batching. Content insertion techniques are useful because they buy us time. This time can be used for time-sharing or in conjunction with merging to increase the catch-up window or alternatively, in the event of failure give a fallback allowing us to wait until resources become available. In the next section, we discuss why content insertion is critical to overload tolerance.
Figure 3 illustrates how content insertion works in
conjunction with merging to free resources during the catch-up window
as well as to reduce  . Let us take the same case of two streams
as in the previous section.
. Let us take the same case of two streams
as in the previous section.
By accelerating stream 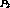 by
setting its content progression rate to
by
setting its content progression rate to 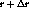 at time
at time  ,
and by additionally inserting alternative content into stream
,
and by additionally inserting alternative content into stream  from
from
 to
to 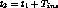 we can make the two streams reach
the same point in the program at time
we can make the two streams reach
the same point in the program at time 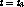 .
. 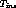 should
be less than the maximum acceptable duration,
should
be less than the maximum acceptable duration,  of inserted
content at any one time. Let
of inserted
content at any one time. Let 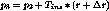 be
the position of stream
be
the position of stream  at time
at time  . The catch-up window is now
given by
. The catch-up window is now
given by
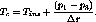
It is possible to also set the content progression rate of stream  to
to  at time
at time 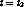 and make the streams reach the
same point in the program earlier, at time
and make the streams reach the
same point in the program earlier, at time 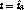 and the merging
time interval
and the merging
time interval 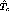 in this case is given by,
in this case is given by,
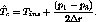
However, 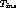 cannot exceed
cannot exceed  as this would lead to an
oscillatory situation with the accelerated stream reaching a point in
time ahead of the stream it is trying to catch up with. This yields the
inequality :
as this would lead to an
oscillatory situation with the accelerated stream reaching a point in
time ahead of the stream it is trying to catch up with. This yields the
inequality :
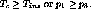
If this condition is violated, then the inserted content must be stopped
abruptly in order to cluster the streams. Hence we can obtain
the following bound on 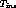 :
:
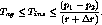
A similar bound can be achieved for 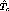 , when the rate of
both streams are being altered. This bound helps us to determine the
feasibility of merging two streams using content insertion. If no
insertion clip can be inserted into the stream in its entirety, the
streams are allowed to merge, without any new content being inserted.
This choice would be a policy decision, based on the system
specifications.
, when the rate of
both streams are being altered. This bound helps us to determine the
feasibility of merging two streams using content insertion. If no
insertion clip can be inserted into the stream in its entirety, the
streams are allowed to merge, without any new content being inserted.
This choice would be a policy decision, based on the system
specifications.
Consider two streams that are spaced two minutes apart in a given
program that must be clustered. This can be achieved by two
minutes of content insertion into the leading stream and a channel is
released in two minutes. With rate adaptive merging, clustering takes
much longer. If we accelerate the trailing stream by 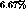 ,
,
 then the streams spaced
two minutes apart would be clustered in 30 minutes. In addition, if
we decelerated the leading stream, clustering occurs in 15 minutes. This
is an unacceptably long time for overload recovery!
then the streams spaced
two minutes apart would be clustered in 30 minutes. In addition, if
we decelerated the leading stream, clustering occurs in 15 minutes. This
is an unacceptably long time for overload recovery!
However, rate adaptive merging would still be required to fine tune the clustering process. Suppose that the inserted content is in the form of 30 second clips and there are several content insertion channels such that a clip starts on some content insertion channel every 5 seconds. Content insertion can be done smoothly only if the temporal skew between streams are exactly integral multiples of 5 seconds and the failure or interaction that triggers clustering is aligned with the start of an insertion clip, both of which are unlikely to happen. However, these small fractional skews from the start of the clips can be eliminated by the use of rate adaptation.
Content insertion can be applied to overload situations in an
entirely different way as well. Consider a server that has a capacity
to serve 1,000 channels and the system demand requires the existence
of 1,025 streams. If we ignore merging and focus on content insertion
alone, assuming that we have content insertion channels, we can
switch 25 streams on to these channels for 60 seconds. Streams
can be vacated in rotation and the cycle would complete in 40
minutes. Thus streams would receive an ad-dosage of 1 minute
once every 40 minutes. In the event that continuous resource reclamation
is carried out using merging, the situation would improve vastly. If the
contrary is true, and the overload increases, it would result in degradation
of service manifested as an increased amount of inserted content. We
refer to this situation as stream-thrashing. Arguments similar
to overload in time-shared operating systems come to bear -- there
are always intrinsic checks and balances that would reduce popularity
with service degradation on overload. Section 5 describes additional
advantages due to content insertion.
Section 5 describes additional
advantages due to content insertion.
In this section, we formalize our model based on the concepts
introduced in Section 2 and apply it to analyze
recoverability under failure and propose schemes for recovery
under different overload scenarios. Table 1 describes the notation
used in the paper.
describes the notation
used in the paper.
Let the total number of servers in the cluster be N and the servers
are denoted by 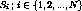 . Let
. Let  denote
the cluster. To simplify analysis, we assume that all streams have identical
bandwidth requirements. However, the maximum bandwidth of each server can be
different in the case of a heterogeneous server cluster. Without loss
of generality we can use the bandwidth of a single stream as a unit of
server bandwidth.
denote
the cluster. To simplify analysis, we assume that all streams have identical
bandwidth requirements. However, the maximum bandwidth of each server can be
different in the case of a heterogeneous server cluster. Without loss
of generality we can use the bandwidth of a single stream as a unit of
server bandwidth.
Let 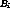 be the total bandwidth of the server
be the total bandwidth of the server  in terms of the
number of streams that the server can support. Let
in terms of the
number of streams that the server can support. Let 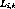 be the
load on server
be the
load on server  at instant t, in number of streams. The total
bandwidth
at instant t, in number of streams. The total
bandwidth  available in the system is given by
available in the system is given by 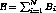 . The total load
. The total load 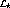 of the
system at instant t, is given by
of the
system at instant t, is given by 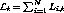 . During normal operation,
. During normal operation, 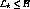 and
violating this constraint constitutes an overload.
and
violating this constraint constitutes an overload.
Let 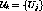 be the set of clients in the system at time
t and
be the set of clients in the system at time
t and 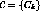 be the set of channels in the system. Let
the set of active streams in the system at time t be
be the set of channels in the system. Let
the set of active streams in the system at time t be 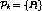 . If channels are reclaimed continuously by merging, then two
streams will carry the same program if and only if there is a temporal
skew between them. The total number of clients
. If channels are reclaimed continuously by merging, then two
streams will carry the same program if and only if there is a temporal
skew between them. The total number of clients 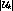 can be
greater than or equal to the number of streams
can be
greater than or equal to the number of streams 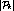 .
Typically
.
Typically 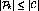 , and violation of this constraint
constitutes an overload.
, and violation of this constraint
constitutes an overload. 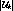 can exceed
can exceed 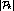 by
virtue of clustering. The global state of the system at any given time
t is given by the following maps :
by
virtue of clustering. The global state of the system at any given time
t is given by the following maps :
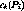 is injective and assigns each stream to a channel and a server. It is
given by
is injective and assigns each stream to a channel and a server. It is
given by  .
.
 .
. 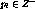 is the position
of the stream
is the position
of the stream  within the program and the state of the session
within the program and the state of the session 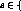 normal playback, accelerated playback, fast forward, rewind, paused,
vacated
normal playback, accelerated playback, fast forward, rewind, paused,
vacated 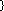 .
.
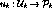 assigns a client to a given stream.
assigns a client to a given stream.
We also require that the following fundamental primitives, that enable the server to control the client, are available. They are necessary in order to implement the functions of merging and content insertion.
ReassignStream(StreamId, CurrentServerId,
NewServerId)
SwitchChannels({ClientId}, CurrentChannelId,
NewChannelId)
Let 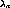 and
and  respectively denote the mean rate of
generation of new streams due to program requests and the average
number of streams that leave the system due to program termination in
the system. Let
respectively denote the mean rate of
generation of new streams due to program requests and the average
number of streams that leave the system due to program termination in
the system. Let  be the mean merging rate, which is the
average number of streams that get merged across all servers in unit
time and let
be the mean merging rate, which is the
average number of streams that get merged across all servers in unit
time and let 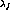 be the mean forking rate, which is the
average number of streams that break away due to client interaction
across all servers. Thus
be the mean forking rate, which is the
average number of streams that break away due to client interaction
across all servers. Thus  , the rate at which channels are
released in the system, is given by
, the rate at which channels are
released in the system, is given by 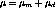 , and
, and
 , the rate at which channels are consumed in the system, is
given by
, the rate at which channels are consumed in the system, is
given by 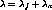 . The stability
criterion requires that
. The stability
criterion requires that 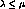 . This is the steady
state referred to later, in Section 3.3.
. This is the steady
state referred to later, in Section 3.3.
In Section 2, we surveyed the basic techniques for resource reclamation. In this section, we develop a fault model that enables us to apply the techniques of merging and content insertion to recover from the overload arising due to failures. We then introduce our proposed procedure to handle different levels of overload. In the context of the server architecture described in Figure 1, the fault monitor and storage are also assumed to be inherently fault-tolerant. This is a reasonable assumption when storage is an independent component. For enhancing fault tolerance, the stream fault monitor which checks for the health of all streams must be implemented as an independent component. However it is possible to implement the monitoring function distributed among the servers with some loss of reliability.
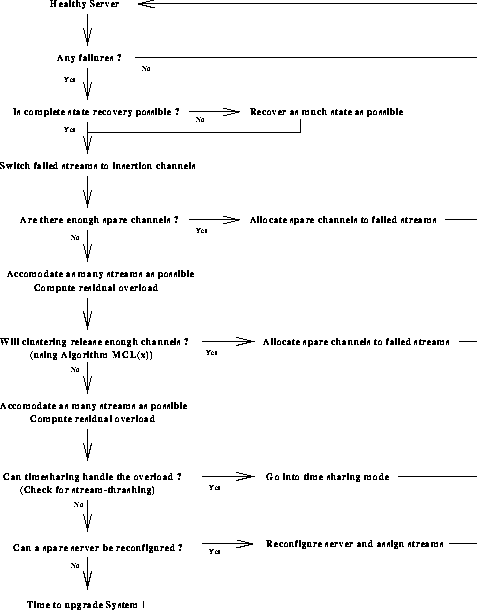
Figure 4: Overload Recovery Procedure
Let us assume that at most q out of N servers in the cluster can
fail simultaneously and that no additional failures occur during the
recovery period. Restoring
service to the failed streams in the event of a failure requires
knowledge of the state of each individual streams that were being
served by the q servers that failed. This can be achieved in
several ways:
Restoring
service to the failed streams in the event of a failure requires
knowledge of the state of each individual streams that were being
served by the q servers that failed. This can be achieved in
several ways:
A fixed number of channels that broadcast advertisements or other alternative content continuously are assumed to be continuously available. In the event of a server failure, the failed streams are transferred to these channels before recovery. This is necessary because :
The procedure for handling overload on failure is shown in Figure 4. We consider several overload scenarios and show how we can handle situations not only when there are more clients than channels, but also when there are more streams than are channels! The first step of the overload recovery procedure involves restoration of stream states. On failure of servers, the failed streams are vacated to content insertion channels as a reflex response. As a first measure, if there are spare channels available, they are allocated to as many streams as possible. The next attempt is to recover channels by clustering. This is solved by the algorithm proposed in the next section which determines the maximum number of clusterings possible within a given amount of time. If the channels released are insufficient to handle the overload, the overload is handled by time-sharing of the channels. If the time-sharing approach is not viable, we configure additional servers to handle the overload. If there is an overload beyond this, the failure is considered catastrophic and streams must be dropped according to a suitable pricing policy (not considered in the paper.)
Given that there is a fault monitor in place and content insertion channels are available, we analyze the conditions that permit partial or complete recovery from the overload, in the next section. The bandwidth consumed by the content insertion channels is negligible and is not considered in the analysis. Also, content insertion channels are distributed across all servers and some of them are available even during failure conditions. We also consider soft-failure when there is no server failure but there is a transient overload resulting from increased interactivity. A solution based on time-sharing of the channels via content insertion into streams in a round-robin fashion is proposed to handle transient overload.
Let us assume that the system is in the steady state before the fault
occurs at time 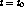 . Let
. Let 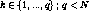 , be
the number of simultaneous server failures where q is a design parameter
of the system. Let
, be
the number of simultaneous server failures where q is a design parameter
of the system. Let 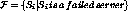 . Clearly
. Clearly  .
This failure generates an extra load
.
This failure generates an extra load 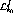 that must be
accommodated, given by
that must be
accommodated, given by 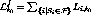 . The loss of bandwidth in the system is
. The loss of bandwidth in the system is 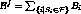 . Thus the bandwidth available after
failure is
. Thus the bandwidth available after
failure is 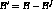 .
.
Case 1 :
Complete recovery is guaranteed for all streams if net overload is
lower than spare bandwidth after failure. This is the trivial case,
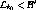 , when the system has spare
bandwidth to accommodate the extra load due to failure.
, when the system has spare
bandwidth to accommodate the extra load due to failure.
Let 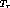 be the computation time required for resource allocation and
be the computation time required for resource allocation and  be the startup latency associated with starting up a stream. We assume that
these are small finite constants in the order of a few seconds. The failed
streams will have or content insertion for a period
be the startup latency associated with starting up a stream. We assume that
these are small finite constants in the order of a few seconds. The failed
streams will have or content insertion for a period 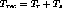 seconds. This is also the recovery period for the entire system. This
represents the baseline user penalty on failure.
seconds. This is also the recovery period for the entire system. This
represents the baseline user penalty on failure.
If there is not enough bandwidth available to reassign all the failed streams to new channels, then a procedure to recover from the residual overload is discussed in Case 2.
Case 2 :
Complete recovery is guaranteed if total load after clustering is lower than the total bandwidth after failure. Clustering of streams involves both content insertion and rate adaptive merging. Content insertion is more powerful and is a coarse grained technique as described in Section 2.4.
We now formulate the clustering problem that handles the overload
scenario of Case 2. Suppose the system can support X channels after
failure, and there are x failed streams that have been switched to
content insertion channels. Without loss of generality we can assume
that that all X channels are currently in use and therefore, we need
to release x within a maximum time to recover, 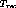 . If
all X channels were not in use, we can assign the available free
channels to as many failed streams as in Case 1 and thereby reduce it
to Case 2. The time to recover,
. If
all X channels were not in use, we can assign the available free
channels to as many failed streams as in Case 1 and thereby reduce it
to Case 2. The time to recover, 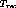 represents the maximum
content insertion period for clients.
represents the maximum
content insertion period for clients.
The solution to the problem first involves determining whether it is
possible to release x channels within 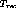 and if not,
what is the maximum number of channels that can be released by
clustering. The solution must also include the list of streams that
are to be clustered together. If less than x channels can be
released by clustering, we release as many as possible and handle the
net overload after clustering by a different mechanism using
time-sharing channels. This would be the Case 3 scenario explained
later.
and if not,
what is the maximum number of channels that can be released by
clustering. The solution must also include the list of streams that
are to be clustered together. If less than x channels can be
released by clustering, we release as many as possible and handle the
net overload after clustering by a different mechanism using
time-sharing channels. This would be the Case 3 scenario explained
later.
We now propose an algorithm called EMCL(x) which takes the number of channels, x, that are required to be released as an argument and returns a list of clusters to release x or more channels. If x channels cannot be released, then EMCL(x) returns a list of clusters which release the maximum number of channels possible. We claim and prove that EMCL is correct and it executes in polynomial time.
Definition 1: Given two streams  and
and 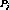 , we define the distance between
them
, we define the distance between
them 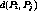 as the time needed to cluster
as the time needed to cluster  and
and 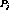 to release a
channel. If
to release a
channel. If  and
and  carry different programs then
carry different programs then 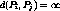 .
.
Definition 2: A cluster, denoted by 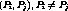 is a group of streams
carrying the same program such that every stream in the cluster has a
program-position in between and including that of streams
is a group of streams
carrying the same program such that every stream in the cluster has a
program-position in between and including that of streams  and
and 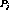 and such that
and such that 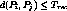 . The size of the cluster
. The size of the cluster
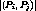 is the number of streams in the cluster and at the end of
clustering,
is the number of streams in the cluster and at the end of
clustering, 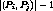 channels would be released.
channels would be released.
Definition 3: The cluster 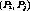 is the earliest in a given program if there
is no other cluster
is the earliest in a given program if there
is no other cluster  such that
such that 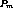 has a program-position
earlier than that of
has a program-position
earlier than that of  .
.
Definition 4: A cluster  is a maximum cluster for a given program, if
is a maximum cluster for a given program, if
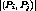 is maximum for that program.
is maximum for that program.
Definition 5: A cluster 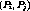 is maximal if there exists no
is maximal if there exists no 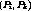 such
that
such
that 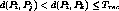 . It is the set of all streams
leading
. It is the set of all streams
leading  that
that  can be clustered with, in time
can be clustered with, in time 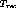 .
.
For the sake of analysis we assume that no two streams considered for clustering are in identical positions in a program. The EMCL algorithm is quite straightforward. It picks the earliest maximal cluster which is largest across all movies and adds it to the list of clusters. This process is continued until we have picked as many or more than the requested number of streams to be merged, or until no more streams can be clustered. The largest cluster across all movies is chosen so that the loop terminates earlier when only a small number of channels are required.
Theorem 1: (Complexity) EMCL(x) runs in polynomial time.
Proof : Suppose every stream in 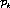 is indexed numerically
and the position of each stream in the program it carries is also
known. We can sort the list of streams by the program index and
then by increasing order of positions. Using a counting sort, this
would take
is indexed numerically
and the position of each stream in the program it carries is also
known. We can sort the list of streams by the program index and
then by increasing order of positions. Using a counting sort, this
would take 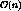 time in terms of the number of streams, n,
in the system. The set S in line 3 can then be constructed in
time in terms of the number of streams, n,
in the system. The set S in line 3 can then be constructed in
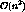 time. Lines 4, 5 and 7 take
time. Lines 4, 5 and 7 take 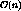 time
while lines 1, 2, 6, 8 and 9 take
time
while lines 1, 2, 6, 8 and 9 take 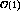 time.
Since the loop in lines 4 -- 9 might be performed at most
time.
Since the loop in lines 4 -- 9 might be performed at most
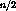 times which is the maximum possible number of clusters
with n streams. Therefore this loop has an overall complexity
of
times which is the maximum possible number of clusters
with n streams. Therefore this loop has an overall complexity
of  . Thus EMCL(x) has a polynomial time asymptotic
complexity,
. Thus EMCL(x) has a polynomial time asymptotic
complexity,  .
. 
Theorem 2: (Correctness) EMCL(x) returns a list that gives at least x clusterings whenever such a set exists. Otherwise EMCL(x) returns a list which corresponds to the maximum number of clusterings that are possible.
Proof : Suppose there are n streams in the system and at most
 clusterings are possible. Assume that EMCL(
clusterings are possible. Assume that EMCL( ) returned
only
) returned
only  clusterings where
clusterings where 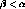 .
. 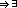 at least one stream
at least one stream  which could have been clustered with
some other stream
which could have been clustered with
some other stream 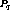 but was not returned by EMCL(
but was not returned by EMCL( ). Let
). Let 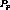 be the first such stream in some program. If
be the first such stream in some program. If 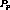 was the very first
stream carrying that program, then
was the very first
stream carrying that program, then  is part of a maximal
cluster. Also, since
is part of a maximal
cluster. Also, since 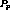 is the very first stream in the program,
it would be part of the earliest maximal cluster which would have been
picked up before the loop in lines 4 -- 9 of the algorithm
terminated. However since it was not returned, it implies that no
such
is the very first stream in the program,
it would be part of the earliest maximal cluster which would have been
picked up before the loop in lines 4 -- 9 of the algorithm
terminated. However since it was not returned, it implies that no
such 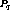 exists, which contradicts the assumption that
exists, which contradicts the assumption that 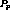 could have been clustered.
could have been clustered.
If 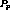 is also the last stream in the program, any stream
is also the last stream in the program, any stream 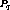 with which it could have been clustered is already part of another
maximal cluster. Since this cluster is maximal it could not have
included
with which it could have been clustered is already part of another
maximal cluster. Since this cluster is maximal it could not have
included 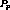 . Therefore, if
. Therefore, if 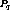 were clustered with
were clustered with 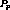 , then
it could not have been clustered with its present group. So the
number of clusterings would remain the same, either way. This means
, then
it could not have been clustered with its present group. So the
number of clusterings would remain the same, either way. This means
 cannot be lesser than
cannot be lesser than  .
.
If 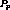 was somewhere in the middle and suppose there existed
a stream
was somewhere in the middle and suppose there existed
a stream 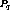 with which it could be clustered. If
with which it could be clustered. If  was earlier
than
was earlier
than 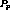 , we can apply an argument similar to when
, we can apply an argument similar to when 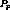 was the
last stream to prove that
was the
last stream to prove that  cannot be lesser than
cannot be lesser than  .
If
.
If 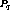 was later than
was later than 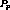 , then
, then  would have been part of
an earliest maximal cluster and would have been chosen. This contradicts
our assumption. Thus EMCL(
would have been part of
an earliest maximal cluster and would have been chosen. This contradicts
our assumption. Thus EMCL( ) would return
) would return  clusterings
if that was the maximum number possible.
clusterings
if that was the maximum number possible.
If asked for more than the maximum, the algorithm will still return
the maximum by virtue of line 8. If asked for less than the maximum,
it may return a list that results in more clusterings than requested,
since the clusters chosen may not add up exactly to what is requested.
Thus EMCL(x) is correct. 
Choosing the earliest maximal cluster is key to our algorithm's correctness. Greedy algorithms which cluster nearest streams pair-wise [6] or those which pick the maximum cluster first can easily be shown to be sub-optimal by trivial counter-examples. Choosing the earliest cluster also offers a distinct advantage. The algorithm would work equally well if we defined maximal clusters around group leaders in the inverse direction and pick the latest maximal cluster instead. However there is little advantage to be gained by clustering streams which are going to terminate soon anyway. By clustering streams that are in the earlier part of the program, the gains are valid for a longer period, provided there are not many break-aways due to interactions.
Though it is possible to refine the algorithm further to improve
performance and to check for violation of per-user constraints, these
are not relevant in the context of this presentation where we mainly
wish to show that we can compute in reasonable time the extent of
recovery from overload that can be achieved via clustering. We
present another algorithm MCL(x), which is a refinement of EMCL(x),
that runs in 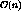 time and lends to direct implementation.
MCL(x) differs from EMCL(x) in that it does not necessarily pick the
earliest cluster first. The complexity analysis is trivial and
correctness of this algorithm follows from Theorem 3.
time and lends to direct implementation.
MCL(x) differs from EMCL(x) in that it does not necessarily pick the
earliest cluster first. The complexity analysis is trivial and
correctness of this algorithm follows from Theorem 3.
Theorem 3: The set S at line 11 in MCL(x) corresponds to the maximum possible number of clusterings.
Proof: Omitted for brevity. 
To simplify analysis, we neglected the possibility of interaction
during clustering. However this does not affect the performance or
correctness of our algorithm. Suppose  interactions occur
during clustering, we can handle them by vacating
interactions occur
during clustering, we can handle them by vacating  arbitrary
streams in the system that are not being clustered currently and
handle the interactions with these channels. The vacated streams are
transferred on to content insertion channels. We also invoke
EMCL(
arbitrary
streams in the system that are not being clustered currently and
handle the interactions with these channels. The vacated streams are
transferred on to content insertion channels. We also invoke
EMCL( ) to release
) to release  channels to restore the channels
that were vacated. If however,
channels to restore the channels
that were vacated. If however,  channels are not available
this represents an overload condition that cannot be handled by
clustering and this condition is handled in Case 3 by means of
time-sharing available channels.
channels are not available
this represents an overload condition that cannot be handled by
clustering and this condition is handled in Case 3 by means of
time-sharing available channels.
Case 3 :
If total load after clustering is marginally higher than the total bandwidth after failure, we can increase the virtual bandwidth of the system by switching clients to content insertion channels in rotation. This is basically time sharing of available channels. The situation is analogous to a multiprocessor system where the number of processes slightly exceeds the number of processors and therefore the percentage of time that each process is idle is small and the interval between idle periods is large. With this technique, there is a risk of stream thrashing, that is, when clients are vacated to content insertion channels very often.
In the same way that processes spend more time swapping than in computation when an operating system thrashes, during stream thrashing the users ``feel'' that they are getting more inserted content than the actual program being watched. Therefore the Case 3 overload problem is one in which we determine if it is possible to handle the overload by time sharing. This technique is also suited to handle transient overload arising when a lot of clients interact simultaneously.
When used in conjunction with Case 2, all streams that are currently
being clustered should not be part of time-sharing. Suppose the system
can support X channels over and above those which are being
clustered. Let x streams be the residual overload which means we need a
virtual bandwidth of X +x streams out of a real bandwidth of
X streams. Suppose 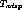 is the minimum time interval
between two content insertion periods for any user. Let us also
neglect prior content insertion if any. Time sharing involves vacating
x streams in rotation and the cycle completes approximately in time,
is the minimum time interval
between two content insertion periods for any user. Let us also
neglect prior content insertion if any. Time sharing involves vacating
x streams in rotation and the cycle completes approximately in time,
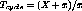 . Overload can be handled without stream
thrashing provided
. Overload can be handled without stream
thrashing provided 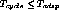 . If this is violated,
we have the scenario outlined in Case 4.
. If this is violated,
we have the scenario outlined in Case 4.
Case 4 :
If we determine that stream-thrashing is imminent, by applying the
analysis in Case 3, it is still possible to recover from the overload
gracefully, provided we can reconfigure spare servers into the system
to handle the overload before stream-thrashing becomes apparent. If the
time to reconfigure a spare server is  the system can recover
gracefully if
the system can recover
gracefully if 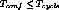 . If spare servers cannot be
configured, the overload cannot be absorbed completely and some streams
must be dropped.
. If spare servers cannot be
configured, the overload cannot be absorbed completely and some streams
must be dropped.
In this section, we quantify the gains that can be obtained by using the proposed mechanism. We first consider timesharing of channels which depends only on the number of streams and can therefore be computed accurately. Figure 5 shows the gains from timesharing. The intersection of each curve with the horizontal axis corresponds to the capacity of a server. For example, a server capable of delivering 1000 streams can support about 1200 streams with a 10 minutes of inserted content every hour. In modern television programming in the USA, commercial advertisements of up to 16 minutes per hour are common, therefore, the stated gains of 20% or more are realizable. The variation of ad-dosage with server capacity and different levels of overload is shown in Figure 6. This analysis can be used to decide the operating point of the server based on expected overload levels.
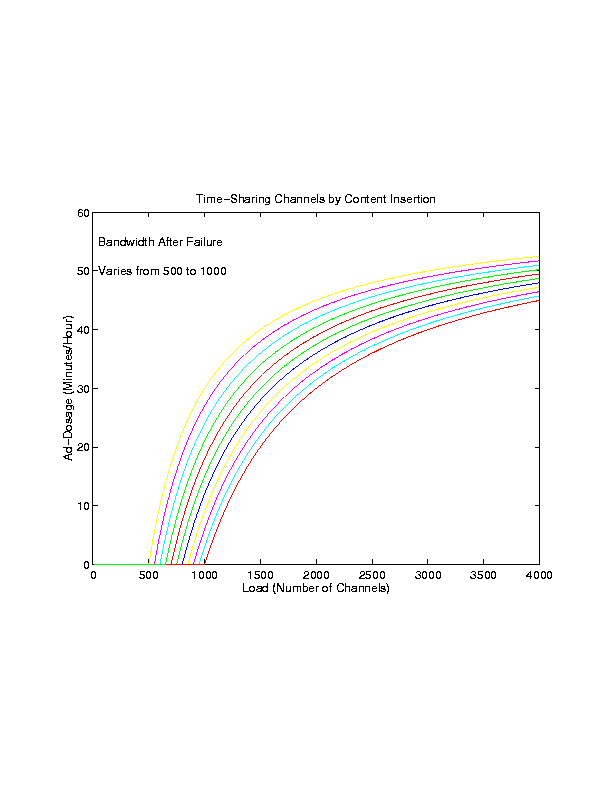
Figure 5: Timesharing for Failure Recovery

Figure 6: Ad-dosage for Given Capacity and Overload
Gains from rate adaptive merging have been studied in detail by Golubchik et al. [6]. However these gains are over an extended merging period. We implemented the MCL algorithm to evaluate the gains from clustering in overload scenarios where there is a limitation on the time available for merging. For this simulation we varied the number of streams watching the same movie of length 30 minutes. The streams were initially distributed randomly along the length of the movie using a uniform distribution. We then invoke the MCL algorithm to release the maximum number of channels possible for recovery periods of 1, 2, 4 or 8 minutes. The results of this simulation are shown in Figure 7. For example, if 50 viewers are watching the same 30 minute clip at a given time, then using just one minute of inserted content, about 10 channels can be released, which translates to a gain of 20 %.
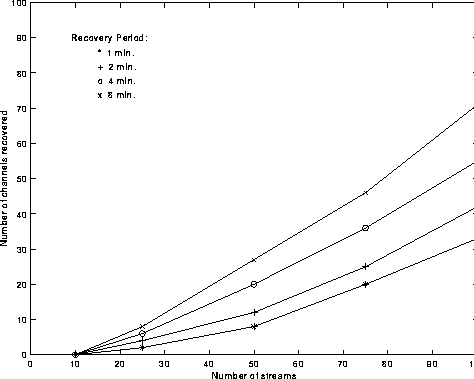
Figure 7: Channel Recovery using MCL
If an interval caching policy [4] is implemented on each server, the stream allocation strategy might try to optimize cache usage by placing mergeable streams on the same server. Unfortunately these streams share the same fate in the event of server failure. This reduces the possibility of channel reclamation and therefore overload recovery. This situation can be avoided by allocating streams that can be clustered across different servers. While this may be suboptimal from the caching perspective, it does not affect gains from clustering and will improve overload tolerance. As an alternative to content insertion channels, clips for insertion can be stored entirely in the cache.
In our paper live transmissions are irrelevant for the following reason. We need only one channel for each live broadcast. Streams which are at any temporal skew from the live broadcast are not ``live'' by definition. Assuming content is being spooled, replays would be permissible within the content that has been spooled. This spooled content represents just another program in the system for all practical purposes.
Although with rate adaptive merging, it is possible to decelerate the rate of the leading stream, it is not practical when there are a large number of trailing streams that we want to cluster with it. Also, practical considerations favor that we handle only the normal and accelerated content progression rates. In the introduction we stated that merging involves processing overheads. A practical solution for supporting rate adaptive merging of streams from content stored in a single format with negligible processing overhead for MPEG encoded streams is proposed in [7]. We can therefore justify the use of merging to perform fine-grained clustering.
Clearly, content insertion improves on merging as resources are freed earlier than merging as described in Section 2.4. The other advantage is the use of ad revenues to offset the cost to the user. In this case the ads are also subsidizing costs in an entirely new way by permitting aggregation. A third advantage is that the technique can be applied to schemes other than merging. Content insertion techniques can also be applied to handle transient overload phenomena. Interactions cause clients to break-away from their groups, defeating the gains that are made via batching [5]. Since each break-away claims a new channel, with a finite probability, the system can be depleted of all channels. This causes future interactions to block. The clustering algorithm described can be used to recover resources. Some of the criteria that can be used to determine the events that trigger the clustering algorithm include :
Clustering involves degradation of quality of service to the customer and it is necessary that the clustering policy is fair to all the customers. Therefore, the content-insertion policy must ensure that each customer receives no more than the maximum allowed advertisement time ( ad-dosage) and no less than a minimum ad-dosage so that advertising revenue objectives can be satisfied. Customers should get an equitable distribution of the total ad-dosage. Most importantly, customers should experience no less than a specified minimum period between advertisements. If this is violated on average, then it is an indication of stream-thrashing in the system. Finally we note that it is reasonable to implement an overload recovery scheme that avoids Case 2 in the interest of simplicity and handles overload directly using Case 3 and Case 4. However, Case 2 is attractive as it can handle a higher degree of overload and represents a potential mechanism to increase system utilization during peak loads.
Since merging and content insertion result in service degradation, we define a user penalty metric which is composed of three different components : the duration of inserted content that the user must tolerate, the duration that content is delivered at an altered rate, and the interval between two content insertion periods. Rate adaptation can be done without significant loss of perceived quality while content insertion is clearly obvious. Users are sensitive to the frequency of content insertion and it is desirable to space them as widely apart as possible. Therefore the components are weighted differently to reflect this fact. The penalty on the overall system is the average penalty for all users in the system and the objective is to minimize this quantity while trying to maximize the number of streams supported. Fairness considerations require that the variance in user penalty among users be as low as possible. We can ensure that constraints for all users are met by pessimistically scheduling the constraints. In other words, we can make aggregation and vacation decision on groups based on constraints corresponding to the most limiting users in the group.
The penalty function is given by 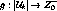 ,
where
,
where  is the set of non-negative integers. We assume a digital
system in which time is counted in discrete steps. For the given user
is the set of non-negative integers. We assume a digital
system in which time is counted in discrete steps. For the given user 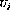 ,
let
,
let 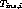 ,
, 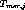 and
and 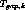 respectively
denote the duration of the
respectively
denote the duration of the 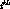 content insertion, the duration of the
content insertion, the duration of the
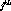 merging interval and the gap between the
merging interval and the gap between the 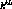 and
and 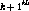 content insertions. The penalty function is then defined by,
content insertions. The penalty function is then defined by,
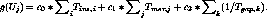
Server performance is indicated by the maximum number of clients that
can be supported by the system for a given average client penalty
averaged over all clients in the system. The objective is to minimize
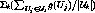 .
.
Other useful indicators are the time to recover from overload and the packing density which is the average of the ratio of the number of clients to the number of streams. Since scheduling is cyclic in most continuous media servers [1], each data point is a single scheduling cycle. A high packing density means that we can increase the number of clients and hence the revenue. On the negative side, it also means a higher chance of transient overload. It is possible to honor per-user penalty by making each group adopt the constraints of the most limiting user in the group. However this may not provide the globally optimal system utilization. In an earlier section, we analyzed the extent of overload recovery that can be achieved within a given maximum time interval. Some per-user constraints may be violated during overload since the recovery algorithms do not evaluate the user penalty function. However we can pre-filter the streams for which constraints may get violated and take them out of the scope of the recovery algorithms.
A possible enhancement to the proposed scheme is the use of metadata to determine suitable insertion points to prevent vacations from occurring at inappropriate moments. Another enhancement would be to to combine the scheme with knowledge of user profiles in order to tailor the inserted content.
Overload recovery in CM servers differs from that in conventional servers due to the requirement of continuity in playout. In this paper we showed that clustering by merging and content insertion can be applied to provide graceful recovery and overload tolerance on failure in CM servers. We proposed a procedure which can handle different degrees of overload efficiently and in a practical manner. We also provide a linear time algorithm to determine whether clustering can release the required amount of bandwidth. We also showed how classical ideas of time-sharing in multiprocessor systems can be applied to handle transient overload phenomena. We have presented a linear time algorithm which determines the maximum number of clusterings possible within a fixed recovery period.
We have discussed how content insertion when applied to resource reclamation and overload recovery can subsidize user costs in an entirely novel and significant way. Future work in this area includes determination of optimal subclustering within the clusters in order to use the minimum bandwidth during clustering as well as integration of the proposed mechanism in a VOD server prototype implementation. While the domain of discourse in the paper is overload scenarios in clustered CM servers, the techniques proposed can easily be adapted to other domains such as congestion or failure in the network.