Highly Scalable Image Coding for Multimedia Applications

ACM Multimedia 97 - Electronic Proceedings

November 8-14, 1997

Crowne Plaza Hotel, Seattle, USA

Highly Scalable Image Coding for Multimedia Applications

Jie Liang
Media Technologies Lab
Digital Signal Processing R&D Center
Texas Instruments, Inc.
P.O.Box 655303, MS 8374
Dallas, TX 75265
email: liang@ti.com phone: (972) 997-6015

ACM Copyright Notice

Abstract:

In this paper, we will present a highly scalable wavelet image codec that also achieves good coding efficiency, both subjectively and in terms of PSNR (Peak Signal-to-Noise Ratio). A proposal based on this codec was recently adopted as the texture coding mode in the MPEG4 Working Draft (WD). This codec supports embedded scalability at many SNR levels and spatial resolutions without sacrificing image quality, and the scalability is supported all the way to lossless compression (compressed once, and decoded at multiple resolutions and qualities according to end users' needs without transcoding). We will introduce in detail the techniques used in the codec. The syntax of the MPEG4 texture coding mode that incorporates this technology will also be introduced. This highly scalable image codec is an enabling technology for many multimedia applications. In this paper, we will describe some of the applications made possible with this technology, such as efficient progressive transmission for web browsing, dynamic rate shaping by network routers, flexible image storage and management in digital cameras, and efficient texture mapping using compressed images in computer graphics.

Keywords

ACM Multimedia, Electronic Proceedings, Image Coding, Scalability, Wavelets.

Tabel of Contents

Introduction

Efficient image coding methods are essential for many multimedia and communications applications. There are many challenges to overcome for a good image codec, such as coding efficiency, implementation simplicity, scalability, low delay, and low power consumption. For instance, in internet web browsing applications, the limited available bandwidth puts strict restraints on the coding efficiency of the image codec. At the meantime, good scalability is a key feature so that the web server can easily and rapidly adjust the bitrate to be transmitted in order to accommodate the wide range of network bandwidth fluctuations. As more and more portable and hand-held devices demand video capability, a good codec suitable for those applications should also be easy to implement and need minimal power consumption.

In recent years, a family of very efficient image coder based on wavelet hierarchical decomposition has been developed and emerged as one of the most promising techniques to meet the aforementioned challenges for image coding. The idea of grouping wavelet coefficients at different scales and predicting zero coefficients across scales was first developed by Shapiro. In [1], Shapiro introduced an embedded zero-tree wavelet coding scheme (EZW) that not only has provided excellent coding performance, but also has fully embedded bit stream (i.e., the bit-stream of a lower bitrate is embedded in the bit-stream of higher bitrates) and is easy to implement. His work has since generated a lot of interest and has been shown to be one of the most efficient image coding methods around.

Many researchers have since worked on variations of the original zero-tree method. In [2], the bit-plane encoding of the significant coefficients is replaced with direct quantization and entropy encoding of the nonzero coefficients. As in EZW, the positions of the significant coefficients are encoded with hierarchical trees. The locations of the zero wavelet coefficients at higher bands are predicted from zero coefficients at lower bands. However, by directly quantizing the significant coefficients, the highly desirable embedded property is lost.

In [3], Said and Pearlman also built on the idea of exploiting the correlation among the amplitudes of related coefficients at different scales and proposed a coding scheme they called Set Partitioning in Hierarchical Trees (SPIHT). Instead of scanning the zero-tree from subband to subband and labeling the nodes as zero-tree root (ZTR), isolated zero (IZ), positive significant (POS) or negative significant (NEG), their SPIHT method uses the concept of set partitioning to code the location of nonzero coefficients. The descendants of a given coefficient at a lower subband are considered as a set in a list of insignificant sets (LIS). Once a significant coefficient emerges from this set, the set is further decomposed. Though the idea of SPIHT is similar to EZW in that they both try to exploit the inter-scale correlation and partial ordering of the coefficients, the scanning order of the significant coefficients and the way of encoding their positions are quite different.

The idea of hierarchical zero-tree is studied with a statistical framework in [4], and an image compression method is proposed that uses morphological representation of wavelet coefficients. Other issues of EZW algorithms have also been studied in the literature. For instance, a variation of Shapiro's EZW algorithm that is more amenable to channel errors is described in [5]. The parallel implementation of the embedded zero-tree method is discussed in [6]. There is also work in the area of efficient VLSI implementation of EZW algorithms [7].

In this paper, we propose a novel wavelet image coding algorithm that improves the results of the EZW-based algorithms through better context modeling for arithmetic coding, improved symbol set for zerotree encoding, better base band compression with DPCM (Differential Pulse Code Modulation) coding. This new algorithm maintains the basic structure and all the nice features of the original EZW algorithm and yet significantly improves its coding performance.

For instance, the algorithm is highly scalable in both PSNR quality and resolutions, that is, from one single coded bitstream, we can extract compressed bitstreams that represent the original coded images at various subjective qualities at various resolutions, with a trivial amount of processing and no transcoding. Our algorithm supports scalability at various resolutions while the original EZW algorithm of Shapiro as well as the SPIHT algorithm supports fine granularity of scalability only for images decoded at the original resolution. Another distinctive feature of the this codec is that it supports continuous scalability all the way to lossless compression. Its lossless compression performance is competitive with the best non-scalable lossless compression algorithm while achieving good coding efficiency at low bitrates. Using the first frame of the standard test sequences used in MPEG4 evaluations, we compare the coding results from this new codec and the results from our implementation of Shapiro's EZW algorithm. With the same wavelet filter and the same number of decomposition levels, we observe an improvement of 1.0 db to 2.0 db in peak signal to noise ratio (PSNR) for a wide range of bitrates. The visual quality is better as well.

MPEG4 is an emerging video coding standard aimed at multimedia applications. After rigorous testing and evaluations, the ISO/IEC MPEG4 standardization committee selected an algorithm that incorporates the wavelet codec described in this paper as the texture coding mode for the encoding of texture, images and documents due to its good coding efficiency and high scalability [8]. We will outline and briefly discuss the syntax of the MPEG4 texture coding mode in this paper. The multiresolution representation and highly scalable bitstream produced by this wavelet image codec are useful in many multimedia applications. In this paper, we will describe some of its potential applications in areas such as efficient progressive transmission for web browsing, dynamic rate shaping by network routers, flexible image storage and management in digital cameras, and efficient texture mapping using compressed images in computer graphics.

Multiresolution Representation
and Wavelet Transforms

The idea of representing a signal at multiple resolutions was the centerpiece for many techniques used in multimedia applications. For instance, the presence of a multiscale representation facilitates efficient image database browsing, texture mapping for a natural and synthetic images (e.g. Mip mapping in graphics), and pattern recognition using scale-space operations. Unlike Discrete Cosine Transforms (DCT) or Fourier Transforms (FFT), wavelet transforms offer a natural decomposition of signals at multiple resolutions without the penalty of overheads, i.e. the number of wavelet coefficients are exactly the same as the number of samples in a signal. This great feature of wavelet transform leads itself to natural fit with many of the existing techniques in signal processing, graphics and pattern recognition. The relationship of wavelets and multiresolution representations can be illustrated in the following framework [9].

Let $V_{0} \supset V_{1} \supset V_{2} \supset \ldots$ be a sequence of nested subspaces from a fine scale to a coarse scale. Each subspace V_k-1 can be written as the direct sum of the subspace at coarser scale V_k and its orthogonal complement W_k.

$\begin{displaymath} V_{k-1}=V_{k} \oplus W_{k} \end{displaymath}$

A multiresolution decomposition of V₀ can be given as

$\begin{displaymath} V_{0}=W_{1}\oplus W_{2} \oplus W_{3} \oplus \ldots \oplus W_{N} \oplus V_{N} \end{displaymath}$

(1)

Let $\phi_{mn}$ and $\psi_{mn}$ be the orthonormal bases for the subspaces V_m and W_m respectively, where

$\begin{displaymath} \phi_{mn}=2^{ -\frac{m}{2}} \phi(2^{-m} t-n) \end{displaymath}$

$\begin{displaymath} \psi_{mn}=2^{ -\frac{m}{2}} \psi(2^{-m} t-n) \end{displaymath}$

Since the functions $\psi_{mn}$ form a basis for $W_{m}, \ m=1,2, \ldots, N$ , the collection of all these functions $\psi_{mn}$ plus the basis functions $\phi_{Nk}$ in V_N will constitute an orthonormal basis in the space V₀. The basis functions $\phi_{mn}$ are related by the scaling equation:

$\begin{displaymath} \phi (t)= \sqrt{2} \sum_{n} h_{n} \phi(2t-n)\end{displaymath}$

(2)

Also,

$\begin{displaymath} \psi(t)= \sqrt{2} \sum_{n} g_{n} \phi(2t-n)\end{displaymath}$

(3)

The functions $\psi_{mn}$ are called the wavelets. The requirement that $\phi(t)$ is orthogonal to $\phi(t-k),k=1,2,3,\ldots$ leads to the Nyquist condition:

$\begin{displaymath} \sum_{n} h_{n}h_{n-2k} = \left\{ \begin{array} {cc} 1 & k=0 \ 0 & otherwise \end{array} \right.\end{displaymath}$

(4)

A sufficient condition for $\phi(t)$ being orthogonal to $\psi(t)$ is:

g_n=(-1)ⁿ h_-n+1
(5)

When we decompose a function f in the wavelet basis $\psi_{j,k}$ , we need to calculate the inner product $< f, \psi_{j,k} \gt$ . From equations (2) and (3), we have:

which tell us that we can get the coefficients $< f, \psi_{j,k} \gt$ by convolving the coefficients $<f, \phi_{j-1,k} \gt$ with g_-n followed by decimation by 2. Recalling the structure of QMF filter banks [10], the above procedure suggests that if we start with the coefficients of the wavelet representation at the finest scale and pass them through a QMF filter bank with filters whose impulse responses are h_-n or g_-n (the relations (4) and (5) are exactly the same as the conditions we have for QMF filter banks), then the outputs of the filter bank at different stages are just the coefficients of the decomposition at different scales. In this way, the representation of the original signal by the wavelet functions $\psi_{j,k}$ can be computed in O(N) operations for a length N signal. Figure 1 illustrates the pyramid decomposition procedure, where $s^{j}= <f,\phi_{j,k} \gt$ and $d^{j}= <f,\psi_{j,k} \gt$ .

**Figure 1:** The Pyramid decomposition
$\begin{figure} \centerline{ \psfig {figure=bank_pyramid.eps,height=1.8in} }\end{figure}$

In practice, we usually use the discrete signal directly as the input to the filter banks instead of the coefficients $<f, \phi_{0,n}\gt$ . We pass these coefficients through the filter bank as described before and get the representations at different scales. We may consider the above pyramid decomposition procedure as a discrete orthogonal transformation in its own right without reference to continuous time signals (just as we can view DFT as a linear transform in the discrete-time domain without reference to the continuous Fourier transform). Unlike in the continuous time domain where the wavelet functions $\psi_{mn}$ are just shifted and scaled versions of each other, the basis vectors in a discrete wavelet transform are related by filtering and decimation. The practice of applying the pyramid decomposition directly on the input signal, instead of its decomposition at some fine scale, is also referred to as the empirical wavelet transform by some researchers. One shortcoming of the wavelet transform is its sensitivity to translations. Some recent work has addressed this problem effectively [11,12].

The Predictive Embedded Zero-Tree Wavelet Coding Algorithm

The embedded zero-tree (EZW) algorithm was originally introduced by Shapiro in his celebrated paper [1]. Since then, many researchers have investigated similar ideas and zero-tree based image codecs are still currently among the state of art for still picture coders. In a wavelet image codec, wavelet transform is first applied to the input image to decorrelate the image data and to obtain a multiscale representation of the input. The contribution of the embedded zerotree algorithm is the observation that strong correlation exists in the amplitudes of the wavelet coefficients across scales, and its efficient solution for taking advantage of these cross-scale correlations.

The EZW algorithm is essentially a coding algorithm using the idea of partial ordering. After the wavelet transform, the significant (nonzero) coefficients are encoded from the most significant bit (MSB) to the least significant bit (LSB). The wavelet coefficients are partially ordered in such a way that each time a group of wavelet coefficients with amplitudes in the range of T₀[ 2^-k-1, 2^-k ) are added to the list of significant coefficients with k decreasing. Thus, the coefficients added in a prior pass are always larger than the coefficients added in a later pass. The encoded bitstream is therefore also naturally prioritized with the more significant bits coded before the less significant bits. To recover the encoded signal at the decoder, we also need to send the positions of the nonzero coefficients as side information. This side information could be a significant portion of the total bit count. The novelty of Shapiro's zero-tree algorithm is that by exploiting the inter-scale correlation among wavelet coefficients at the same location, the overhead for sending the position information can be greatly reduced.

In this paper, we introduce a new wavelet coding algorithm that improves the performance of the EZW method with several extensions. The coding performance can be improved significantly with the introduced modifications. Next, we describe the algorithm in some details, and then elaborate on some of the extensions that have been introduced.

The Algorithm

The relationship among the wavelet coefficients can be illustrated by Figure (2). A wavelet coefficient at a lower frequency band is related to four wavelet coefficients in the immediate higher subband with the same orientation. The four coefficients at the higher band are called the children of the coefficient at the lower band, which is in turn called the parent. Every coefficient is related to some other coefficients at the same spatial location by this parent and children relationship.

**Figure 2:** The parent-child relationship of wavelet coefficients
$\begin{figure} \centerline{ \psfig {figure=parent_child.eps,height=2.5in} }\end{figure}$

Let $w_{k}, k=0,1,\cdots, N-1$ be the wavelet coefficients of a input signal. C is the maximum value of the amplitudes of all the coefficients, i.e.

$\begin{displaymath} C = \max_{0 \le k \le N-1} \vert w_{k}\vert \end{displaymath}$

We select an initial threshold T₀ which can be written as

$\begin{displaymath} T_{0}=\alpha 2^{E}\end{displaymath}$

(6)

where E is an integer, and $\alpha$ is a constant, such that

$\begin{displaymath} T_{0} \le C < 2 T_{0}\end{displaymath}$

(7)

The threshold T_i is halved after each pass, so that

$\begin{displaymath} T_{i} = \alpha 2^{E-i}\end{displaymath}$

(8)

As in the EZW quantization, the Predictive EZW (PEZW) quantization starts with a dominant pass through the wavelet decomposition tree from low subbands to high subbands. Each coefficient w_k is compared with the threshold T_i. The coefficients are classified into four categories as follows:

Zero Tree Root with Zero value (ZTRZ):
if |w_k| < T_i, all of its descendants are zero or symbol X.
Zero Tree Root with Significant value (ZTRS):
if $\vert w_{k}\vert \ge T_{i}$ , all of its descendants are zero or symbol X.
Isolated Zero (IZ):
if $\vert w_{k}\vert \ge T_{i}$ , and at least one of its descendants is not zero.
Isolated Significant coefficient (IS):
if $\vert w_{k}\vert \ge T_{i}$ , and at least one of its descendants is not zero.

If a coefficient is classified as ZTRS or IS, it is removed from the list of insignificant coefficients and put into the list of significant coefficients. If labeled as IS, the coefficient is then labeled with symbol X (a don't care symbol). In subsequent dominant passes, the coefficients labeled with X are treated in two different ways: (1). they are ignored, and no bits are sent, because we already know that they are significant for the current threshold; (2). they are treated as a Zero, if by interpreting them as such, a zerotree root (ZTRZ or ZTRS) at a coarser scale will be formed. No overhead bits are needed to distinguish between these two cases because the occurrence of (2) will exclude the occurrence of (1). After encoding symbols ZTRS and IS, one extra sign bit is also sent.

The dominant pass is followed by a subordinate pass. In the subordinate pass, one more bit is sent or encoded for each of the coefficients in the list of significant coefficients. Equivalently, we can say the interval which contains the true amplitude of the coefficient is halved in size. Then, the threshold T will be halved, and the whole procedure starts over again until the threshold reaches a preset minimum or the bit count reach a preset bit budget.

In summary, the PEZW quantization can be described as the following steps:

1.: set T_i = T₀/2ⁱ, stop if $T_{i} \le Q$ ,where Q is a predetermined quantization step size, or if the bit count reaches the bit budget.
2.: (dominant pass)

Compare each coefficient w_k with T_k, and classify it as ZTRZ, ZTRS, IZ, IS. Encode the symbols with arithmetic code and the statistical model that corresponds to the current context. Move the coefficient labeled as ZTRS or IS to the list of significant coefficients. Replace the significant coefficient labeled as IS with symbol X. Increment the frequency count of the corresponding symbol by 1.
3.: (subordinate pass)

Send one more bit from each coefficient in the list of significant coefficients to the decoder.
4.: Increase i, initialize the frequency count, and go to step 1.

In the above process, the encoder or decoder can elect to stop whenever a certain constraint such as a bit budget is satisfied. With proper syntax and markers as used in the MPEG4 texture coding mode, for a given compressed bitstream, the decoder can elect to decode (a) the whole bitstream, (b) the first M bits, or (c) all or part of the sub-bitstream that is related to a given spatial resolution. These flexibilities are very useful in many applications as will be discussed in the later part of this paper.

New symbol set for better coding efficiency

In the original EZW algorithms, the wavelet coefficients are coded in several passes. Each pass encodes one bit plane. The positions of the coefficients that become significant with respect to the new threshold are encoded efficiently with zerotrees, in which each node of the tree represents the significance of the coefficient at the node and the coefficients in the subtree rooted at the current node (we could consider a zerotree as essentially a significance map). The original EZW algorithm use the following symbols to represent the significance of the nodes:

$\begin{displaymath} \{ZTR, IZ, POS, NEG\} \end{displaymath}$

where ZTR (Zero Tree Root) represent a node where the coefficient itself is zero and all its descendants are zero, IZ (Isolated Zero) represents a node where the coefficient itself is zero and not all its descendants are zero, POS (POSitive) represents a node where the coefficient itself is positive (regardless of the status of its descendants), and NEG (NEGative) represents a node where the coefficient itself is negative (regardless of the status of its descendants). It can be shown that statistically the zero wavelet coefficients tend to cluster in the same spatial location, and the conditional probability for zero coefficients is much higher given the parent of the coefficient being zero. This explains why the zerotree quantization reduces the overhead for the significance map and provides good coding efficiency.

**Figure 3:** The state transition graph for the symbols that represent the wavelet coefficients. The dashed lines are the transitions that can be derived from parent nodes and therefore require no additional bits.
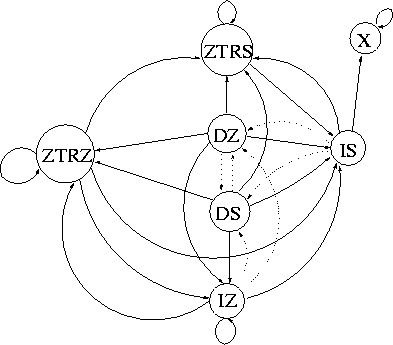$\begin{figure} \centerline{ \psfig {figure=states.eps,height=3in} }\end{figure}$

In this paper, we further improve coding efficiency with a different set of symbols, namely

$\begin{displaymath} \{ZTRZ, ZTRS, IZ, IS\}\end{displaymath}$

ZTRZ (Zero Tree Root with Zero value) represents the node where the coefficient itself is zero as well as all its descendants. ZTRS (Zero Tree Root with Significant value) represents the node where the coefficient itself is non-zero, but all its coefficients are zero. IZ (Isolated Zero) is a node where the coefficient is zero but not all its descendants are zero. IS (Isolated Significant coefficient) represents a significant coefficient whose descendants are not all zero.

In comparison with the original symbols, we replace the POS and NEG symbols with one symbol IS because the possibility for positive numbers and negative numbers are about equal. By using one symbol, we reduce the number of symbols used to reduce complexity and increase accuracy for probability estimation.

In addition, we introduce the ZTRS symbol to make significant coefficients permissible as the root of a zerotree. This addition can be justified with some theoretical analysis. For a given random signal generated by a auto-regressive (AR) process, the frequency spectrum of the AR process is a decaying function with respect to frequency. The rate of decaying must be faster than 1/f. Their wavelet coefficients also decay with respect to scale at similar rate. In [13], it was shown that even for the 1/f signals which exhibit infinite energy, wavelet coefficients also decay with respect to scales. Since in zerotree quantization, at each pass, we halve the threshold. The possibility that a parent node is non-zero while all its descendants are zeros is significant. By introducing the symbol ZTRS, we can efficiently represent all the zero descendants of a non-zero root node. Note that for the original EZW algorithm, we need to first send POS or NEG for the significant coefficients and then send four ZTR symbols to indicate all descendants are zeros. Simulation results also confirms the improvement using the new symbol set. Similar symbols are also used in [2] in the context of non-scalable wavelet coding.

Context modeling and forgetting factors for arithmetic coding

Fixed point arithmetic coding is used to entropy code the zerotree symbols. Arithmetic coding is known to be able to optimally encode a stationary random sequence if the statistics of the random signal can be estimated accurately [14]. In practice, arithmetic coding can provide very good coding performance for small symbol sets, which is the case in our Predictive Embedded Zerotree Coding (at most 4 symbols).

The statistics are estimated with accumulative frequencies. Forgetting factors are used to adjust the adaptation window size of the frequency estimation. The forgetting factor allows the arithmetic coder to adjust to the local statistically. However, too small an adaptation window will fluctuate the statistics too frequently, which in turn degrades the performance. In our algorithm, we choose the forgetting factor to be 127, which empirically gives the best results.

Most importantly, we use context modeling to better estimate the probability distribution of the symbols. The context is determined by two factors:

the state of the coefficient in the previous pass
the subband that the coefficient is in

One of the contributions of this paper is the finding that the probability distribution of the current symbol is highly conditioned on the probability distribution of its state in the previous pass. For instance, if a coefficient is a descendant of a zero zerotree root (ZTRZ) in the previous pass. Then its probability of being zero in the current pass is significantly higher than in the case where it is the descendant of a significant zerotree root (ZTRS). Fig. (3) illustrates the state transition graph for a coefficient from a previous pass to the current pass. The additional symbols DZ,DS are for internal use only, where DZ refers to the descendant of a ZTRZ symbol, DS refers to the descendant of a ZTRS symbol.

The probability distributions for the various subbands are also quite different. For instance, for the highest subband, there will be no zerotree roots. When we initialized the frequency count for the highest subband, we set the frequency count for ZTRZ, ZTRS to be zero, because they will not appear in that subband.

For the subordinate pass, the probability for 1 or 0 is about equal. Therefore, we could elect to use no entropy coding for the subordinate pass. In our algorithm, we use arithmetic coding to gain a bit more efficiency. The frequency count is initialize d to be:

$\begin{displaymath} freq\_sub = [1,1] \end{displaymath}$

which represents frequency count for 1 and 0 respectively.

**Figure 4:** Prediction of base band wavelet coefficients
$\begin{figure} \centerline{ \psfig {figure=DPCM.eps,height=3in} }\end{figure}$

DPCM coding for base band coefficients

We separate the base band (LL band) coefficients from the higher band coefficients and code them with DPCM coding. The motivation is the observation that the statistics of the base band signal is very different from those of the higher bands. For instance, the amplitudes of the base band coefficients tend to be much larger with bigger variance, reflecting the DC fluctuation of the corresponding blocks. When we start the zero-tree quantization with an initial threshold determined from the maximum amplitude of all coefficients, we usually need a lot more passes than we will need if we take the base band out of the zero-tree scanning. Experiment results show that we save bits for zero-tree quantization by taking the base-band out of the zero-tree. Since the neighboring coefficients are more correlated in the base band than in the higher bands, it is more efficient and makes more sense to code the base band with DPCM coding than with bit plane coding.

Given an $M \times N$ image and a decomposition level of l, the size of the decomposed image in the baseband is of the size $\frac{M}{2^{l}} \times \frac{N}{2^{l}}$ . For the Intra frame of a standard QCIF sequence as used in MPEG4 testing, with a decomposition level of 4 for the luminance component and 3 for the chrominance component, the baseband is essentially an image of the size $9 \times 11$ for both the luminance and chrominance components. The wavelet coefficients at the base band can be looked at as the DC levels of the local blocks they correspond to. There is strong correlation among neighboring coefficients. Differential coding in this situation can reduce the variance of the coefficients, and encode the coefficients more efficiently.

There have been a lot of research done in the area of differential coding. In this report, we adopt a simple adaptive DPCM coder that has been used in the MPEG4 Verification Model. First, all the wavelet coefficients in the base band are scalar quantized with a preset quantization step size Q. Then, the quantized value of a current coefficient w_X is predicted from three other quantized coefficients in its neighborhood, i.e. w_A, w_B and w_C (see Figure (4)), and the predicted value is subtracted from the current coefficient. That is,

$if \ (\vert w_{A}-w_{B}\vert) < \vert w_{B}-w_{C}\vert)$
$\hat{w}_{X}=w_{C}$
$w_{X} = w_{X} - \hat{w}_{X}$
else
$\hat{w}_{X}=w_{A}$
$w_{X} = w_{X} - \hat{w}_{X}$

The coefficients after the DPCM are then encoded with arithmetic coding.

Lossless Compression

By using integer wavelet transforms such as S-Transform, TS-Transform, and S+P Transform instead of floating point wavelet transforms [15,16], the same algorithm can be extended to lossless coding. The bitstream is scalable from very low bitrate to lossless coding continuously. Table 1 shows its lossless compression performance for the USC image data set using S+P transform. Compared with another well-known scalable wavelet lossless coding algorithm CREW [15], our results are about $2.6\%$ better, while maintaining good coding efficiency at low bitrates (as shown in section 6).

**Table 1:** Lossless compression results (bits/pixel)
$\begin{displaymath} \begin{tabular} {\vert\vert c\vert c\vert c\vert c\vert c\ve... ...08 & 5.86 & 4.59 & 4.73 & 3.30 & 4.52 \ \hline \end{tabular} \end{displaymath}$

MPEG4 Texture Coding Mode

MPEG4 is a video coding standard that is currently being developed by the ISO/IEC MPEG standardization committee. Unlike its predecessors MPEG1 and MPEG2 which are primarily developed for broadcasting and entertainment applications, MPEG4 is developed with the requirements of many multimedia applications under considerations. The capability of compositing complex multimedia scenes that are composed of video, audio, graphics and documents is a distinguished feature of the MPEG4 standard. The need for texture and image coding tool inside the MPEG4 standard is therefore also highly desirable. After rigorous testing and evaluation, the MPEG4 committee selected a wavelet based coding algorithm that incorporates the PEZW algorithm we have described in the paper [8]. Figure (5) illustrates the structure of the codec. In the following, we briefly introduce the texture coding mode used in MPEG4. Please note that the MPEG4 standard is on-going, and the syntax is subject to change.

As in the PEZW algorithm, the MPEG4 texture codec encodes the base band coefficients separately after the wavelet transform. The user has the choice of three different quantization mode: (1) the bi-level quantizer mode, (2) the single quantizer mode, and (3) the multiple quantizer mode. The bi-level quantizer mode is essentially the PEZW algorithm. It provides maximal scalability (many levels of scalability at multiple resolutions). The single quantizer provides limited scalability but quick in speed. The multiple quantizer mode is a tradeoff of (1) and (2), namely a predetermined level of scalability for reduced computational complexity.

**Figure 5:** MPEG4 Texture Coding Mode
$\begin{figure} \centerline{ \psfig {figure=wvtcodec.eps,height=1.8in} }\end{figure}$

The following is the syntax of the texture coding mode:

Still_image_object_layer() {

stillimage_object_layer_start_code (28 bits)

stillimage_object_layer_id (4)

stillimage_object_layer_shape (2)

if(stillimage_object_layer_shape == 00) {

stillimage_object_layer_width (16)

stillimage_object_layer_height (16)

}

wavelet_decomposition_levels (8)

Y_mean (8)

U_mean (8)

V_mean (8)

Quant_DC_Y (8)

Quant_DC_UV (8)

for (Y, U, V){

lowest_subband_bitstream_length (16)

lowest_subband_texture_coding()

}

spatial_scalability_levels (5)

quantization_type (2)

SNR_length_enable (1)

for (Y, U, V){

for (i=0; i<spatial_scalability_levels; i++)

spatial_bitstream_length (24)

if (quantization_type == 0)

; single quantizer mode

Quant (8) (note: skipped for V)

wavelet_zero_tree_coding()

}

else if quantization_type == 1) {

; multiple quantizer mode

SNR_Scalability_Levels (5)

(note: skipped for U,V)

for(i=0;i < SNR_scalability_levels; i++){

Quant (8) (note: skipped for V)

if(SNR_length_enable == 1)

SNR_bitstream_length (10 or more)

wavelet_zero_tree_coding()

}

else {

; bi-level quantizer

Quant (16)

if (SNR_length_enable == 1)

SNR_bitstream_length (10 or more)

wavelet_zero_tree_coding()

}

next_start_code()

}

There are several markers and flags in the bitstream that are added to enhance the scalability of the bitstream:

SNR_length_enable: If this flag is enabled ( disable =0; enabled = 1), each SNR scale (bit plane ) starts with a field in which the size of the bit stream for that SNR scale is determined. By putting the length of each bitplane in the bitstream, we can extract the bits that belong to a certain bit plane. Also we can take out the bits that belong to the same bitplane but a different scale, reassemble them and form a new bitstream which represents the original images at different resolutions and SNR qualities.

spatial_bitstream_length: This field defines the size of the bitstream for each spatial resolution in bits.

SNR_bitstream_length: This field defines the size of the bitstream for each specific SNR scale. The format is as the following:
extension (1 bit) | length (9 bits)
and the following scripts shows how the bitstream length is coded:

while ( bitstream_size / 512 > 0 ){

extension = 1;

put mod(bitstream_size, 512) in length

bitstream_size = bitstream_size>>9;

}

extension = 0;

put `bitstream_size' in length

Note that for any bitstream coded with the MPEG4 texture codec in the bi-level quantizer mode, we can always decode the subset of the bitstream that has already been transmitted and obtain a representation of the original image, albeit at lesser quality.

Coding Results

In this section, we present some I frame coding results using some of the standard MPEG4 test images. The test sequences, i.e. Akiyo, Container Ship, and Hall Monitor, are all in QCIF format, namely, $176 \times 144$ in size, and in 4:2:0 color format. We use 4 levels of decomposition for the luminance and 3 levels of decomposition for the chrominance. The wavelet filter used is the 9-3 tap Daubechies filter [17]. The bitrates are calculated using the actual size of the bitstream file. The PSNRs are computed using the reconstructed images from the decoder. The comparisons are shown only on luminance, with the PSNRs for chrominance the same for both our method and the original EZW method.

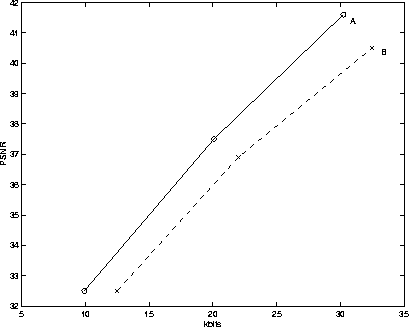
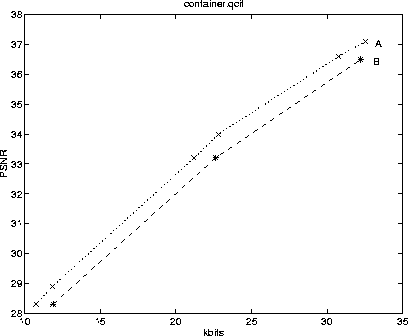
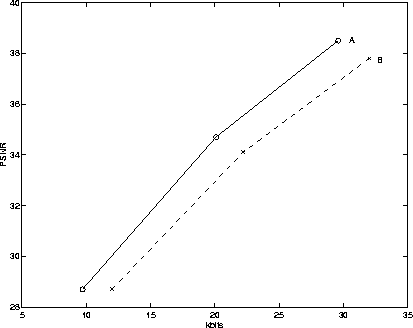
Figure (6), Figure (7), and Figure (8) show the PSNRs for the first frame of the three sequences using both methods. We can see that our new method has an improvement of 1 - 3 db for all three sequences for a wide range of bitrates (from 10kb to 30 kb). The improvement is more pronounced at higher bitrates. The visual quality is better as well.

**Figure 6:** Coding results for the I frame of the Akiyo sequence. curve A: using the new wavelet algorithm. curve B: using Shapiro's EZW algorithm.
$\begin{figure} \centerline{ \psfig {figure=akiyo.eps,height=3in} }\end{figure}$

**Figure 7:** Coding results for the I frame of the Container sequence. curve A: using the new wavelet algorithm. curve B: using Shapiro's EZW algorithm.
$\begin{figure} \centerline{ \psfig {figure=container.eps,height=3in} }\end{figure}$

**Figure 8:** Coding results for the I frame of the Hall Object sequence. curve A: using the new wavelet algorithm. curve B: using Shapiro's EZW algorithm.
$\begin{figure} \centerline{ \psfig {figure=hall.eps,height=3in} }\end{figure}$

Applications

In this section, we elaborate on the application of the PEZW image codec in some multimedia applications such as web browsing, dynamic rate shaping, and computer graphics.

Web Server and Browsing

The most annoying problem with net-surfing today is the delay caused by limited bandwidth, with a lot of them caused by heavy use of graphics and images in the web pages. This problem is not likely to alleviate soon because any increase in bandwidth is likely to be offset with even more wide-spread use of large size images and graphics by content providers.

A good way of accelerating the down-loading of images and graphics is the use of highly scalable image codec. The original image could be coded at high bitrate and fine resolution, and be stored on the web server. Then the server can provide different versions of the image to different users according to their respective bandwidths, or the images can be progressively transmitted to the end user while they are doing other jobs. A good, efficient scalable image coder is hence essential in this scenario.

The widely used JPEG coding standard indeed has a scalable profile that can provide a certain level of scalability. However, the limited scalability comes with a loss in coding efficiency. In addition, no spatial resolution scalability are supported. In light of this, the MPEG4 texture codec as well as the PEZW algorithm is a natural fit for web server and browsing applications.

The web servers and browsers incorporating the scalable image codec work as follows:

The images are stored on the web server coded with high fidelity, i.e., high resolution, high bitrate, etc.
When a user requests down-loading of the images, the server selects the bitrate according to the bandwidth available and selects the spatial resolution according to the user's preference and bandwidth. Therefore, a user who is using a high bandwidth connection will automatically receive a high fidelity version of the coded image, while a user using a 28.8k modem will receive a lower fidelity version.
The browser will decode the first M bits received and display the image with minimal latency. Note M could be any number here, so the latency is controllable. The image will be refined as more bits come in.

The above procedure will dramatically reduce the latency in web browsing caused by down-loading graphics and images. A Netscape plugin version of the PEZW codec is under development currently. Its potential can be evaluated with the video tape which accompanies this paper.

Dynamic Rate Shaping

In network communications, end-to-end data transmission is accomplished by relaying the data packets along a path of network routers. The bandwidth of the end-to-end connection depends on the bandwidth of all the hops in the data path. On a network where quality of service (QoS) is not guaranteed such as the TCP/IP network, the bandwidth of the connection tends to fluctuate a lot. In a real-time communication application, it is therefore important for the network routers to be able to scale bitrate of the data transmission dynamically. With the PEZW algorithm, the bitstream is embedded and scalable up to bit-level precisions. The network routers could simply discard any packets that are of a lower priority (bit-plane wise or scale wise) and the end-user could still decode the received bitstream. The rate adjustment can be done by the routers in the middle of the path without requesting retransmission.

Texture Mapping

Texture mapping gives realism to computer generated images and speeds up the rendering of a scene. Efficient texture mapping is becoming increasingly important for graphics applications. Mapping compressed images directly saves the on-board memory and enables the mapping of large images. Tallisman is a recent architecture that takes use of JPEG-based compression for texture mapping [18]. The PEZW algorithm can also be applied here to achieve efficient texture mapping.

The Mip texture mapping technique utilizes multiresolution representation of a image to reduce computation in texture mapping [19]. In traditional Mip mapping, a pyramid of images of various resolutions is generated and stored, which can take up to $1\frac{1}{3}$ storage space of the original image. With the PEZW algorithm, the image pyramid is generated by the wavelet transform without oversampling (the number of wavelet coefficients is the same as the number of image pixels), and the codec further compresses the image significantly. In addition to the syntax described above, we will have a lookup table for each 64x64 blocks similar to the chunking technology adopted in Tallisman. The graphic hardware can choose the resolution and quality (bit-plane) according to the view point and decode the needed blocks. This technology enables storing of large size images on the graphic board as well as flexibility in choosing the resolution and quality of image to be mapped. These features are even more important when the scene images are fed real-time through networks such as internet virtual reality or gaming applications.

Conclusions

In this paper, we have proposed a new wavelet coding algorithm that gives excellent coding results. We show that this new algorithm improves upon Shapiro's original EZW algorithm. In the meantime, all the desirable features of the EZW algorithm are maintained. For instance, the new algorithm is highly scalable and has embedded bitstreams, requires no training and VLC tables, is easy to implement, and supports seamless progressive coding ranging from lossy to lossless compression. We also briefly discussed the MPEG4 texture coding mode syntax that incorporates this algorithm. Some applications of this algorithm in multimedia applications are also discussed.

References

1

Jerome M. Shapiro.
Embedded image coding using zerotrees of wavelet coefficients.
IEEE Trans. Signal Processing, 41(12):3445-3462, December 1993.

2

S. A. Martucci and I. Sodagar.
Zerotree entropy coding of wavelet coefficients for very low bit rate video.
Proc. IEEE Int. Conf. Img. Proc., 1996.

3

A. Said and W. A. Pearlman.
A new, fast, and efficient image codec based on set partitioning in hierarchical trees.
IEEE Trans. Cir. Sys. for Video Tech., June 1996.

4

M. T. Orchild and K. Ramchandran.
Wavelet-based image coding using a novel morphological framework.
Proceedings of the SPIE, vol.2491, 1995.

5

C. D. Creusere.
Robust image coding using the embedded zerotree wavelet algorithm.
Proceedings Data Compression Conference, 1996.

6

C. D. Creusere.
Image coding using parallel implementation of the embedded zerotree wavelet algorithm.
Proceedings Data Compression Conference, 1996.

7

Bae Jongwoo and V. K. Prasanna.
A fast and area-efficient VLSI architecture for embedded image coding.
Proceedings Data Compression Conference, 1996.

8

ISO/IEC JTC1/SC29/WG11.
MPEG-4 Video Verification Model Version 6.1.
draft in progress, 1997.

9

Ingrid Daubechies.
Ten Lectures on Wavelets.
SIAM, 1992.

10

P. P. Vaidyanathan.
Multirate systems and filter banks.
Prentice Hall, 1993.

11

J. Liang and T. W. Parks.
A translation invariant wavelet representation algorithm and its applications.
IEEE Trans. Signal Processing, 44(2), February 1996.

12

J. Liang and T. W. Parks.
Image coding using translation invariant wavelet transforms with symmetric extensions.
to appear in the IEEE Trans. Image Processing.

13

Gregory W. Wornell.
Wavelet-based representations for the 1/f family of fractal processes.
Proc. IEEE, 81(10):1428-1450, October 1993.

14

Glen G. Langdon.
An introduction to arithmetic coding.
IBM Journal of Research and Development, 28(2):135-149, March 1984.

15

A. Zandi, J. D. Allen, E. L. Schwartz, and M. Boliek.
Crew: Compression with reversible embedded wavelets.
IEEE Data Compression Conference, Snowbird, UT, March 1995.

16

A. Said and W.A. Pearlman.
An image multiresolution representation for lossless and lossy image compression.
IEEE Transactions on Image Processing, September 1996.

17

A. Cohen, I. Daubechies, and J. C. Feaveau.
Biorthogonal bases of compactly supported wavelets.
Commun. Pure Appl. Math., 45:485-560, 1992.

18

Jay Torborg and James T. Kajiya.
Tallisman: Commodity Realtime 3D Graphics for the PC.
Computer Graphics, 1996.

19

Lance Williams.
Pyramidal parametrics.
Computer Graphics, 17(3), July 1983.

Jie Liang
8/18/1997